序言：看原书第二章后做的笔记，关键术语留有英文注解, 有些内容补充了自己的理解，并非直接翻译原文。

• 本人水平有限，若有不当之处，欢迎交流与指正，谢谢。

• 原书第四版pdf下载链接：Github: t4world/Computer-Graphics
• Markdown 数学公式语法参考: Cmd Markdown 公式指导手册

1 集合与映射

通常，我们所指的函数是映射(mapping)的一种特殊情况。映射是集合A到集合B的一种对应关系。 笛卡尔积(Cartesian product)$A$x$B$是2个集合的元素的所有可能组合，即a$\epsilon$A, b$\epsilon$B,对所有可能的有序组合(a,b)。$A$ x $A$简写为$A^2$,以下常用符号：

符号	意义
$R$	实数
$R^+$	非负实数
$R^2$	2维实数平面
$R^n$	n维实数笛卡尔空间
$Z$	整数
$S^2$	3D单位球面上的点

• 映射的表示方法 使用冒号和箭头,举例: $f: R \rightarrow Z$ 其中前者为定义域(domain),后者为值域(target). 从编程语言的角度来看，也可以认为是 参数为$R$，返回值为$Z$。

1.1 逆映射

通常所说的反函数是一种逆映射。 对于一个映射 $f: A \rightarrow B$,那么可能存在逆映射 $f^{-1} : B \rightarrow A$. 即 对于 $b = f(a)$,有$f^{-1}(b)=a$. 存在逆映射的条件是： 对每一个b$\epsilon$B,存在唯一确定的$a\epsilon A$满足$f(a)=b$.

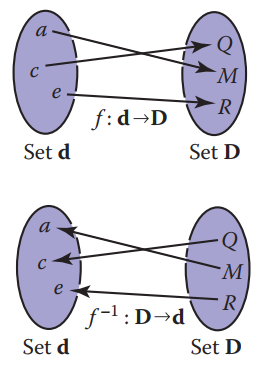
若在满足逆映射的条件下，此时f是函数，(即 对每一个a$\epsilon$A,有唯一确定的b=f(a)),此时这种特殊的映射关系称为双射(bijection), $f$和$f^{-1}$互为反函数，值域和定义域对调。

反函数例子: f: R $\rightarrow$ R,函数f(x)=$x^3$ ,反函数$f^{-1}(x)=\sqrt[3]x$

1.2 区间

关于是否包含区间边界值，分为开区间和闭区间以及半开区间。 涉及到图形的表示，注意，例如表示一个单位立方体的3D区间，立方体内的点$x$可以表示为$x \epsilon [0,1]^3$. 区间还有个方便之处，区间运算，并集(union,符号$\cup$)，交集(intersection,符号$\cap$)，差集(difference,符号-)等。

1.3 对数

对数是相对于指数关系而生的，针对一个底数a，求它的多少次方为x. 表现形式如下： $$y = \log_a x \iff a^y = x $$ 复习几个常用的公式：
$a^{\log_a (x )} = x$
$\log_a {(a^x)} = x$
$\log_a (xy) = \log_a x +\log_a y$
$\log_a (x /y) = \log_a x - \log_a y$
$\log_a x = \log_a b \cdot \log_b x$
有个特殊的底数为$e=2.718…$,用它作底数，那么对数形式则会简写为： $$\ln x \equiv \log_e x$$ 它和指数函数的导数形式分别如下：
$\frac {d}{dx} \log_a{x}=\frac{1}{x\ln a}$
$\frac {d}{dx} a^{x} =a^x \ln a$
$\text{上述公式当a = e 时}, \ln a = 1.$

---

2 求解二次方程

复习一下初中数学知识, 一元二次方程的一般形式： $$Ax^2 + Bx + C = 0,$$ 求根判别式(discriminant)为 $\Delta = B^2 - 4 \cdot A \cdot C$，有三种情况:

1. $\Delta<0:$ 方程没有根
2. $\Delta=0:$ 方程只有一个根, $x_0 =x_1 =\frac{-B}{2A}$
3. $\Delta>0:$ 方程有2个根, $x_0= \frac{-B+\sqrt{\Delta}}{2 \cdot A} , x_1= \frac{-B-\sqrt{\Delta}}{2 \cdot A}$

个人经验：注意, 开方和除法开销昂贵，图形学中为了简化运算，提倡对$x_0,x_1$ ,做简化：
$\text{令 }\Delta _2 = {(\frac{B}{2})}^2- A \cdot C$ , 则 $x_0= \frac{-(\frac{B}{2})+\sqrt{\Delta _2}}{A} , x_1= \frac{-(\frac{B}{2})-\sqrt{\Delta _2}}{A}$

---

3 三角学

3.1 角度

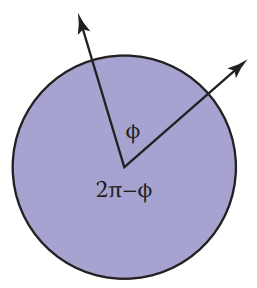
如下图所示，角度由2条射线(half-line)组成,射线将圆分成了2段弧(arc)，弧线长度即为角度大小,角度有正负之分,逆时针方向为正(counterclockwise)，图中的角度 $\Phi$ 即为短的那段弧。按照这样的定义，角度值的取值范围为$[-\pi , \pi]$

• 角度制(degrees)和弧度制(radians)的转换，因为整圆是$360^\circ$,也是弧度制的$2\pi$, 所以角度转换如下： $$degrees = \frac{180}{\pi} \cdot radians$$

3.2 三角函数

说起三角函数，先复习勾股定理(也叫毕达哥拉斯定理，$Pythagorean-theorem$),如下图所示，简单的证明了斜边(hypotenuse)平方为2条直角边的平方和。

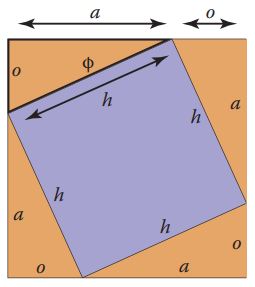
$$a^2 + o^2 = h^2,$$ 由此定义了正弦(sine),反正弦(arc sine),余弦(cosine),反余弦(arc cosine),正切(tangent),反正切(arc tangent).

函数	$\sin \Phi $	$\csc \Phi $	$\cos \Phi $	$\sec \Phi $	$\tan \Phi $	$\cot \Phi $
值	$ o/ h$	$ h/ o$	$ a/h$	$ h/a$	$ o/a$	$ a/o$

涉及到图形学中的方位角(直角坐标和极坐标的映射)，有个实用的函数$atan2$,它比$atan$的数值更稳定,且值域更广，对于一个笛卡尔(Cartesian)直角坐标$(x,y)$如下所示：

$$ atan2(y,x)= \begin{cases} arctan(\frac {y}{x}), & \text { x > 0} \\ arctan(\frac {y}{x}) + \pi, & \text{ $y \geq 0$,x<0} \\ arctan(\frac {y}{x}) - \pi, & \text{ y < 0,x<0} \\ +\frac{ \pi}{2}, & \text{ y > 0,x=0} \\ -\frac{ \pi}{2}, & \text{ y < 0,x=0} \\ undefined, & \text{ y = 0,x=0} \end{cases} $$

以上的函数定义域和值域如下：
$asin : [-1,1] \mapsto[- \pi / 2, \pi /2];$
$acos: [-1,1] \mapsto[0,\pi];$
$atan:R \mapsto[-\pi/2,\pi/2];$
$atan2: R^2 \mapsto [-\pi, \pi]$

3.3 一些有用的特性

• 角度平移特性(高中数学老师说过,"奇变偶不变，符号看象限")
  $\sin(-A) = - \sin A$
  $\cos(-A) = \cos A$
  $\tan(-A) = - \tan A$
  $\sin(\frac {\pi} {2} - A) =\cos A$
  $\cos(\frac {\pi} {2} -A) = \sin A$
  $\tan(\frac {\pi} {2} -A) = \cot A$

• 勾股定理推导特性 ${\sin}^2 A +{\cos}^2 A=1$
  ${\sec}^2 A -{\tan}^2 A=1$
  ${\csc}^2 A -{\cot}^2 A=1$

• 加减特性 $\sin(A +B )=\sin A \cos B + \sin B \cos A$
  $\sin(A -B )=\sin A \cos B - \sin B \cos A$
  $\cos(A +B )=\cos A \cos B - \sin A \sin B$
  $\cos(A -B )=\cos A \cos B + \sin A \sin B$
  $\tan (A+B) =\frac{\tan A + \tan B}{1- \tan A \tan B}$
  $\tan (A-B) =\frac{\tan A - \tan B}{1+ \tan A \tan B}$
  $\sin (2A) = 2 \sin A \cos A$
  $\cos (2A) = \cos ^2 A -\sin ^2 A$
  $\tan (2A) =\frac {2 \tan A}{1 -\tan ^2 A}$

• 半角特性 $\sin ^2 (\frac{A}{2})=(1- \cos A)/2$
  $\cos ^2 (\frac{A}{2}) =(1+\cos A)/2$

• 积化和差 $\sin A \sin B = -\frac {\cos (A+B) -\cos (A-B)}{2}$
  $\sin A \cos B = \frac {\sin (A+B) +\sin (A-B)}{2}$
  $\cos A \cos B = \frac {\cos (A+B)+\cos (A-B)}{2}$

• 三角形特性 对于任意三角形，假设边长为$a,b,c$,三条边的对角分别为$A,B,C$，那么有以下等式： $$\frac{\sin A}{a} =\frac{\sin B}{b} =\frac{\sin C}{c} \text{ (正弦定理)}$$ $$c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos C \text{ (余弦定理)}$$ $$\frac{a+b}{a-b} = \frac{\tan(\frac{A+B}{2})}{\tan(\frac{A-B}{2})} \text{ (正切定理)}$$ $$S_ \Delta = \frac {1}{4} \sqrt {(a+b+c)(-a+b+c)(a-b+c)(a-b+c)(a+b-c)} \text{ (海伦－秦九韶面积公式)}$$ $$\text{或者，令} p = \frac{a+b+c}{2} , S_ \Delta = \sqrt {p(p-a)(p-b)(p-c)}$$

---

4 向量

向量，也称为矢量，通常表示为一段特定长度和特定方向的箭头$\rightarrow$。通常，不会用来表示坐标或位置，而是偏移(offset)或者位移(displacement).

4.1 向量运算

向量加减运算符合平行四边形原则(parallelogram rule),向量加减满足交换律(commutative property),即 $\vec {a} + \vec {b} = \vec {b} + \vec {a}$ . 向量乘法有多种形式，其中，如果$\vec {a}$与数字$k$相乘，$k$为正数则方向不变，$k$为负数则方向相反，长度则乘以$k$的绝对值.例如 $3.5 \vec{a}$,表示方向不变，长度变为原来的3.5倍.

4.2 直角坐标下的向量

对于一个二维向量$\vec {c}$，可以由任意2个不平行的基础向量组合而成： $$\vec {c} = w_a \vec{a} + w_b \vec{b} ,\text{($w_a$,$w_b$是唯一一组常数解)}$$ 那么，如果让这2个基础向量为直角坐标系的横轴$x$和纵轴$y$两个方向上的单位向量,则向量$\vec{a}$表示为： $$\vec a =x_a \vec{x} + y_a \vec{y}$$ 通常为了方便，也会直接用直角坐标$(x_a,y_a)$表示这个向量，或者使用一个列矩阵，$\vec a =\begin{bmatrix} x_a \\ y_a \end{bmatrix}$, 为了书写和印刷方便，也会直接写为它的转置形式 ${\vec a} ^ T=\begin{bmatrix} x_a & y_a \end{bmatrix}$ .

4.3 点乘

向量点乘得到的为标量积,向量$\vec{a}$和$\vec{b}$的点乘为两个向量的长度相乘，再乘以夹角$\Phi$的余弦值。表示为： $$\vec{a} \cdot \vec{b} =\lVert a \rVert \cdot \lVert b \rVert \cdot \cos \Phi$$ 常用：用于计算2个向量的夹角余弦值，进而推算夹角大小。 向量点乘遵守结合律(associative property)和分配律(distributive property): $$\vec {a} \cdot \vec {b} =\vec{b} \cdot \vec{a}$$ $$\vec {a} \cdot (\vec {b} + \vec {c})=\vec {a} \cdot \vec {b} +\vec {a} \cdot \vec {c}$$ $$(k \vec{a})\cdot \vec{b}=\vec{a}\cdot (k\vec{b})=k\vec{a}\cdot \vec{b}$$ 在直角坐标系下，假设有二维向量$\vec{a}=(x_a,y_a)$和$\vec{b}=(x_b,y_b)$，那么两者点乘结果为 $\vec {a} \cdot \vec {b}=x_a x_b + y_a y_b$ . 类似地，如果是三维向量，那么: $\vec {a} \cdot \vec {b}=x_a x_b + y_a y_b +z_a z_b$

4.4 叉乘

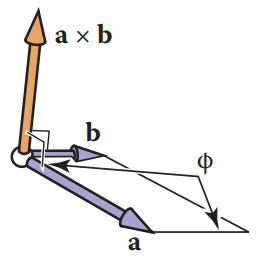
向量叉乘得到的为向量积，通常用于三维向量。 $\vec{a} ,\vec{b}$叉乘向量积的模长为这两个向量的模长相乘，再乘以夹角的正弦值,数值正好等于$\vec{a} ,\vec{b}$围成的平行四边形面积。 $$\lVert \vec{a} \times \vec{b} \rVert=\lVert \vec{a} \rVert \lVert \vec{b} \rVert \sin \Phi ,\text{(且方向同时垂直于$\vec{a} ,\vec{b}$)}$$ 下图为一个右手坐标系

定义$x,y,z$三轴的单位向量分别为： $$\vec{x} =(1,0,0)$$ $$\vec{y} =(0,1,0)$$ $$\vec{z} =(0,0,1)$$ 那么$\vec{x} \times \vec{y}$叉乘结果可以为人为规定为$+\vec{z}$或$-\vec{z}$,这里我们采用$+\vec{z}$，则有： $$\vec{x} \times \vec{y}=+\vec{z}$$ $$\vec{y} \times \vec{x}=-\vec{z}$$ $$\vec{y} \times \vec{z}=+\vec{x}$$ $$\vec{z} \times \vec{y}=-\vec{x}$$ $$\vec{z} \times \vec{x}=+\vec{y}$$ $$\vec{x} \times \vec{z}=-\vec{y}$$ 对右手坐标系的解释：对于$\vec {a} \times \vec{b}$,右手手掌与$\vec{a}$平行，且四指向$\vec{b}$弯曲，此时大拇指所指方向就是叉乘结果$\vec {a} \times \vec{b}$的方向。 注意：常用的$x-y-z$直角坐标系为右手坐标系，即$\vec{x} \times \vec{y}=+\vec{z}$。

叉乘运算满足分配律，结合律(与常数)，但不满足交换律： $$\vec{a} \times (\vec{b} + \vec{c} ) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$$ $$\vec{a} \times (k\vec{b})=k(\vec{a} \times \vec{b}) , \text{ (常数可以提取出来)}$$ $$\vec{a} \times \vec{b} = -(\vec{b} \times \vec{a}), \text{ (一交换则反向)}$$

现在有向量$\vec{a}=(x_a,y_a,z_a)$,或者表示为$\vec{a}=x_a \vec{x} + y_a \vec{y} + z_a \vec{z}$, 另一个向量 $\vec{b} =(x_b, y_b, z_b)$, 那么： $$\vec{a} \times \vec{b} =(x_a \vec{x} + y_a \vec{y} + z_a \vec{z}) \times( x_b \vec{x} + y_b \vec{y} + z_b \vec{z})$$ $$=(y_a z_b - z_a y_b)\vec{x} + (z_a x_b -x_a z_b)\vec{y} +(x_a y_b - y_a x_b)\vec{z}$$ 最终结果也可写作 $\vec{a} \times \vec{b} =(y_a z_b - z_a y_b, z_a x_b -x_a z_b , x_a y_b - y_a x_b )$ .

4.5 标准正交基与坐标系

标准正交基：在2D平面，有互相垂直的一组向量基 $\vec{u} ,\vec{v}$，且都为单位向量，即： $$\lVert \vec{u} \rVert =\lVert \vec{v} \rVert =1, \text{and, }\vec{u} \cdot \vec{v} =0$$ 如果是3D空间，则这组标准正交基$\vec{u}, \vec{v}, \vec{w}$满足：
$\text{(1)} \lVert \vec{u} \rVert =\lVert \vec{v} \rVert =\lVert \vec{w} \rVert =1$
$\text{(2)} \vec{u} \cdot \vec{v} =\vec{v} \cdot \vec{w} =\vec{w} \cdot \vec{u} =0$
$\text{(3)} \vec{w}=\vec{u} \times \vec{v} \text{ (右手坐标系)}$

像这样的正交基 $\vec{u} ,\vec{v} , \vec{w}$有无数组，我们通常默认选用直角坐标轴的单位向量$\vec{x}, \vec{y}, \vec{z}$作为正交基，且原点为$O(0,0,0)$,这样的正则坐标系我们称为世界坐标系(world coordinate system)或全局坐标系(global coordinate system).

有一个物体坐标系$u-v-w$ ,该坐标系中有个向量$\vec{a}$,如果要转换为在世界坐标系下的坐标,使用简单的点乘 即可得到，为 $u_a\vec{u} +v_a\vec{v} +w_a \vec{w}$.

4.6 单个向量构造向量基

设想较为常见的一种情形：给定一个向量$\vec{a}$,我们希望能给出3个互相垂直的正交基$\vec{u},\vec{v},\vec{w}$，要求$\vec{w}$和$\vec{a}$同向,并且不关注$\vec{u},\vec{v}$的具体指向。 分为3步：

• 取$\vec{a}$的单位向量为$\vec{w}$ ，即: $\vec{w} =\frac{\vec{a}}{\lVert \vec{a} \rVert}$
• 任意取一个与$\vec{w}$不共线的向量$\vec{t}$, 两者叉乘后单位化得到$\vec{u}$，即 : $\vec{u}=\frac{\vec{t} \times \vec{w}}{\lVert \vec{t} \times \vec{w} \rVert}$
• 将上述得到的$\vec{w} ,\vec{u}$叉乘得到$\vec{v}$ ，即: $\vec{v} =\vec{w} \times \vec{u}$

书中提到这一场景适用于表面着色，因为法线方向很重要(垂直于表面),着色过程垂直于法线的表面向量无关紧要。

4.7 由两个向量构建向量基

在某些场景需要用2个不共线向量来构建坐标系，比如给定2个互相垂直(perpendicular)的向量$\vec{a}$(指定$\vec{w}$) ,$\vec{b}$(指定$\vec{v}$),则直接叉乘得到第三个向量基$\vec{u}=\vec{b} \times \vec{a}.$

或者，给定的$\vec{a},\vec{b}$并不是完全垂直，而是近似垂直,比如成$80^\circ$角，采用上一节的方法也可以得到最接近的解： $\vec{w} =\frac{\vec{a}}{\lVert \vec{a} \rVert}$, $\vec{u}=\frac{\vec{b} \times \vec{w}}{\lVert \vec{b} \times \vec{w} \rVert}$, $\vec{v} =\vec{w} \times \vec{u} \text{ ,(向量} \vec{v} \text{ 很接近} \vec{b})$ .

获得图形学中相机的Look-At 矩阵/向量也可以采用这一方法，向量$\overrightarrow {direction}$是确定的$from$点到$to$点的向量，而$up$向量和$right$向量就看自己选择了(可以指定Right向量，再来确定Up向量)，这一点在LearnOpenGL-CN中的Camera章节有相关内容。

4.8 摆正向量基

某些场景下可能遇到这样的问题，由于浮点计算精度或者数据保存读取等原因，造成向量基精度丢失，向量基之间不再那么垂直，如何修正是个问题：

可以这样做：基于已有的$\vec{w}, \vec{v}$得到新的$\vec{u}$,然后再计算$\vec{u}$. 虽然得到了精确垂直的新向量基，但是，这并非最好的办法，因为新的向量基$\vec{w}, \vec{v},\vec{u}$和原向量基之间，这3者的误差是不对等的, $\vec{w}$误差最小，$\vec{u}$误差最大。

在本书的第五章第5.4.1 节的奇异值分解可以很好的解决这一问题。

---

5 曲线与面

5.1 2D隐式曲线

先理解一下“隐式”:在我看来，隐式曲线就是隐函数来表示的曲线。隐函数，就是没法用$y=f(x)$来干净清晰的表示函数关系，而是转而使用类似方程$f(x,y)=0$的形式(例如开普勒方程$y-x-\epsilon \sin y=0$,$\epsilon$为常熟)。

为人所熟知的隐式曲线必然是圆了，圆方程$f(x,y)=(x-x_c)^2 + (y-y_c)^2 -r^2$描绘了以$(x_c,y_c)$为圆心，$r$为半径的圆. 对任意的点$(x,y)$值，都可以计算出$f(x,y)$的值，则有：
点在圆内：$f(x,y)<0$;
点在圆曲线上：$f(x,y)=0$;
点在圆外：$f(x,y)>0$;

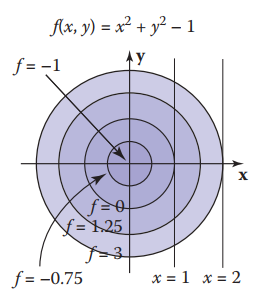
从向量的角度理解，可以认为圆心$c$,圆上的点为$p$, 则向量$\overrightarrow{cp}$模长正好为圆半径$r$，即:$\lVert \overrightarrow{cp} \rVert =r$。 从向量的角度来表示，比原来$x,y,z$之类的坐标表示更易懂，更能体现几何关系，也更不容易在写代码时犯错，尽可能用向量的形式来表示隐式关系。

5.2 2D梯度

假设函数$f(x,y)$是高度场的函数$height=f(x,y)$,那么梯度向量所指的方向就是指向上坡最陡的方向,或者说函数值增长最快的方向。一般是以偏微分的形式 $\nabla f(x,y)$ 给出：

$$\nabla f(x,y)=(\frac {\partial f} {\partial x} \text{ ，} \frac {\partial f} {\partial y} ) .$$

so，偏微分复习：$\frac {\partial f} {\partial x} = lim_{\Delta x \to 0} \frac{f(x+\Delta x , y) - f(x,y)}{\Delta x}$

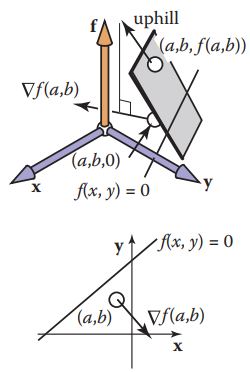
原文图注解：A surface height = f(x,y) is locally planar near(x,y) = (a,b). The gradient is a projection of the uphill direction onto the height = 0 plane.

如上图，对于二维曲线$f(x,y)=0$的点$p(x,y)$,则此时梯度向量垂直于该点的切向量，梯度向量此时为法线向量。

换句话说，把二维曲线$f(x,y)=0$看作是三维曲面$f(x,y)=h$ 被$xoy$水平面截出的等高线，这样上山的最陡路径投影在平面上，正好就是二维曲线的法向方向.

关于这一点，有位知乎答主做了很好的图文并茂的解释，深入理解可以移步$\implies$ 知乎: 形象理解“梯度”与“法向量”的关系 另外，因为梯度指向了上坡方向(uphill),所以指向的是$f(x,y)>0$的区域。

那么，为什么梯度和偏微分有关系呢？下图中，假设在很微小的一个区域，$height=f(x,y)$是一块平面，且向量$\vec{a}$在这个$f$不变的区域移动了一小段距离，即$\vec{a}=(\Delta x,\Delta y)$.因为上坡方向(uphill)垂直于向量$\vec{a}$,即点积为0：

$$(\nabla f)\cdot \vec{a} \equiv (x_\nabla,y_\nabla)\cdot(x_a,y_a)=x_\nabla \Delta x + y_\nabla \Delta y=0 \text{, (式2.5.2-a) }$$

同样地，我们知道$f$的值没有改变，即$\Delta f=0$:

$$\Delta f = \frac {\partial f} {\partial x} \Delta x + \frac {\partial f} {\partial y} \Delta y= \frac {\partial f} {\partial x} x_a + \frac {\partial f} {\partial y} y_a =0$$

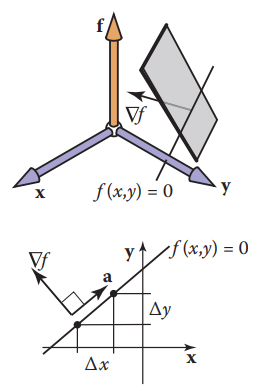
回顾向量知识，如果$(x,y)$ 和 $(x’,y’)$垂直，则$xx’+yy’=0$，(x’,y’)可以取值$(y,-x)$. 那么: $$(x_a,y_a)=k(\frac{\partial f}{\partial y} , - \frac{\partial f}{\partial x}) \text{, (式2.5.2-b) }$$ 根据式子2.5.2-a和2.5.2-b，可以得出: $$(x_\nabla, y_\nabla) = m(\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y}) \text{, (式2.5.2-c) }$$ 通常取k>0,且m=1.

---

• 隐式2D直线(implicit 2D lines)

考虑使用隐函数形式表达一条直线：$Ax+By+C=0$,这种一般形式包含了垂直于$x$轴没有斜率的情况。假设直线上存在两个不同的点$(x_0,y_0), (x_1,y_1)$，则:

$$\begin{cases} Ax_0 + By_0+C =0 \\ Ax_1 + By_1+C =0\\ \end{cases}$$ 很明显，这是个不定方程。 梯度为$\nabla f=(A,B)$, 又因为 $\nabla f$垂直于$(\Delta x, \Delta y)$, 则与 (式2.5.2-c)同理，可以令$\nabla f=(y_0 -y_1,x_1-x_0)$. 替换A，B，则有： $$(y_0 - y_1)x + (x_1 - x_0)y +C =0 \text{, (式2.5.2-d)}$$ 对于(式2.5.2-d)，代入$(x_0,y_0)$，则有$C=x_0y_1 - x_1y_0$: $$(y_0 - y_1)x + (x_1 - x_0)y + x_0y_1 - x_1y_0=0$$ 那么写成"斜率-截距式"(slope-intercept): $$y =\frac{y_1 -y_0}{x_1-x_0}x + \frac{x_1y_0 - x_0y_1}{x_1-x_0}$$

关于隐式表达式的另外一个有趣的属性是可以用来推算点到直线的有向距离，如下图，平行于直线的$f(x,y)$分布于$\pm$两侧。

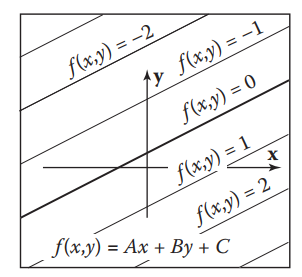
直线之间的距离为梯度的长度，而梯度为k(A,B)，距离则为： $$distance =k \sqrt{A^2 + B^2}\text{, (式2.5.2-e)}$$ $Ax + By+C =0$直线上的点$(x_0,y_0)$,则该点的梯度方向有某点$(a,b)=(x_0,y_0)+k(A,B)$,带入计算： $$f(a,b)=f(x_0+kA,y_0+kB)=k(A^2 +B^2)\text{, (式2.5.2-f)}$$ 综合 (式2.5.2-e), (式2.5.2-f)可知，点$(a,b)$到直线$Ax + By+C =0$的距离： $$distance=\frac{f(a,b)}{\sqrt{A^2 + B^2}}$$

---

• 隐式二次曲线(implicit quadric curves) 对于隐式的2D二次曲线，一般形式可以写作如下： $$Ax^2 + Bxy + Cy^2 +Dx + Ey +F =0$$ 该形式包含了椭圆(ellipse)，双曲线(hyperbola)，抛物线(parabola).

5.3 3D隐式曲面

和2D隐式曲线类似，3D隐式曲面的表达式记作： $$f(x,y,z)=0.$$ 对曲面上任意点$p(x,y,z)$，有$f(p)=0$.

5.4 隐式曲面的表面法线

和2D隐式曲线类似，3D隐式曲面上某点$p(x,y,z)$的法线正好就是该点的梯度: $$\vec{n}=\nabla f(p)=(\frac {\partial f(p)}{\partial x}, \frac {\partial f(p)}{\partial y} ,\frac {\partial f(p)}{\partial z})$$ 并且法线$\vec n$指向的方向为$f(q)>0$的方向(点$q$不在曲面上). 需要注意的是，$f(p)=0$和$-f(p)=0$虽然描述的是同一个曲面，但是法线/梯度方向正好相反：$-\nabla f(p) =\nabla(-f(p))$.

5.5 隐式平面

• 平面可以由一个已知的点$a$和已知的法线$\vec n$来描述 对于平面上任意点$p$： $$(p-a) \cdot \vec n=0$$
• 平面也可以由3个已知的点$a,b,c$来确定 法线可以通过叉乘得到$\vec n=(b-a)\times (c-a)$，对于平面上任意点$p$： $$(p-a)\cdot ((b-a)\times (c-a))=0$$ 写成行列式(determinant)则如下：

$$\begin{vmatrix} { x-x_a}  & {y-y_a} & {z-z_a} \\ {x_b-x_a}  & {y_b-y_a} & {z_b-z_a} \\ { x_c-x_a}  & {y_c-y_a}  & {z_c-z_a} \\ \end{vmatrix}=0$$

• 3D二次曲面(3D quadric surfaces) 2D曲线可以用二元二次多项式$(x,y)$来表示，类似地，3D曲面可以用三元二次多项式$(x,y,z)$来表示。 对于一个球面： $$f(p)=(p-c)^2-r^2 =0$$ 对于一个椭球面(ellipsoid)： $$f(p)= \frac{(x-x_c)^2}{a^2} + \frac{(y-y_c)^2}{b^2} +\frac{(z-z_c)^2}{c^2} -1=0$$
• 由曲面构建曲线(3D curves from implicit surfaces) 如果2个曲面相交，则得到了相交位置的曲线，该曲线的点$p$同时满足： $$ \begin{cases} f(p)=0 ,\\ g(p)=0 .\\ \end{cases}$$

5.6 带参数的2D曲线

带参数的函数：是指自变量$x$和因变量$y$都采用参数$t$表达，点$(x,y)$的位置由$t$来决定，即： $$\begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} g(t) \\ h(t) \end{bmatrix}.$$ 当$t$在连续的改变时，连续函数$g(t),h(t)$也在改变,即点$p(x,y)$在曲线上"移动"了,$t$可以看作是时间，不同$t$区间的(x,y)变化幅度不同，点移动时就会有"速度"的概念。

带参数函数只看变量$t$的这一特性，给相关的程序编写也带来了很大的便利，只有一个函数入参，Cool.

• 带参数的2D直线(2D parametric lines) 2D直线上有2个已知的点$p_0(x_0,y_0),p_1(x_1,y_1)$,那么该直线可表示为： $$\begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} x_0+t(x_1-x_0) \\ y_0+t(y_1-y_0) \end{bmatrix}.$$ 或者采用向量的概念：$p(t)=p_0+t(p_1-p_0)$

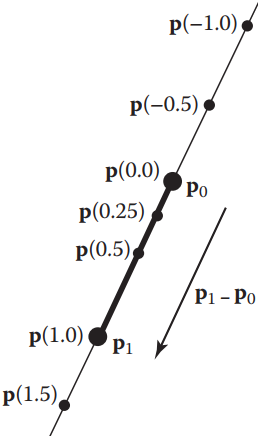
如上图，从几何角度理解为“从p0出发前往p1,具体位置由参数t决定”,且$p(0)=p_0,p(1)=p_1$。所以基于这一点，直线可以表示为从一个定点$origin$出发,移动$t$个单位向量$\vec u$，即： $$p(t)=origin + t \cdot \vec u$$ 而这种表示方法，在光线追踪计算时是表示一条光线的绝佳形式。

• 带参数的2D圆(2D parametric circles) 一个以$(x_c,y_c)$为圆心,$r$为半径的圆，带参数形式可以写作： $$\begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} x_c+ r \cos \Phi \\ y_c+ r \sin \Phi \end{bmatrix}. \text{  (其中$\Phi \in [0,2 \pi)$)}$$ 而一个以$(x_c,y_c)$为椭圆中心,$a,b$为长轴、短轴的椭圆，带参数形式可以写作： $$\begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} x_c+ a \cos \Phi \\ y_c+ b \sin \Phi \end{bmatrix}. \text{  (其中$\Phi \in [0,2 \pi)$)}$$

5.7 带参数的3D曲线

带参数的3D曲线形式如下： $$\begin{cases} x=f(t) \\ y=g(t)  \\ z=h(t) \\ \end{cases}$$ 例如，绕$z$轴的螺旋线如下： $$\begin{cases} x= \cos t \\ y= \sin t  \\ z=  t \\ \end{cases}$$ 本章只阐述3D直线，不详细阐述3D曲线，而是在本书的第15章(Chapter15.Curves)详细阐述。

• 带参数的3D直线(3D parametric lines) 带参数的3D直线可以记作向量的形式，举例如下： $$\begin{cases} x= 2+7t \\ y= 1+2 t  \\ z=  3-5t\\ \end{cases} \quad \text{向量形式$\implies$} \begin{cases} origin=(2,1,3)\\ \overrightarrow {dircetion}= (7,2,-5)  \\ position = origin + t \cdot \overrightarrow {dircetion} \\ \end{cases}$$

5.8 带参数的3D曲面

不同于2D曲面，只有一个参数$t$,3D曲面需要2个参数$u,v$，$x,y,z$都可以表示为$(u,v)$有关的带参数形式：

$$\begin{cases} x= f(u,v) \\ z= h(u,v) \\ \end{cases} \quad \text{向量形式$\implies$} \begin{bmatrix} x \\ y \\ z \end{bmatrix}=p(u,v)$$ 举例：对于一个球面，给定的已知半径$r$，由经度角$\phi$，纬度角$\theta$这2个角度变化确认球面任意点： $$\begin{cases} x= r \cos \phi \sin \theta \\ y= r \sin \phi \sin \theta \\ z= r \cos \theta \\ \end{cases} \quad \text {可以反推} \begin{cases} \theta= arccos(z / \sqrt{x^2 + y^2 +z^2}) \\ \phi = atan2(y,x) \\ \end{cases}$$ 考虑一下曲面的法线呢？ 首先定义函数$q(t)=p(t,v_0)$，此函数u自由变化且v值固定为$v_0$,这就定义了在曲面上的一条曲线，也叫“等参曲线”。(下图采用自AutoDesk工具ALIAS介绍，意义相近)

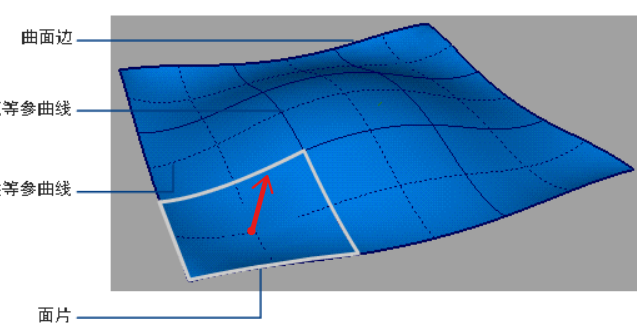
则q的导数$q’$和曲面相切，$q’$为P的偏微分$P_u$，同样地，还可以得到第二条切线$P_v$，那么该点的法线$\vec n$指向曲面外，且同时垂直于这2条曲面切线： $$\vec n = \overrightarrow P_u \times \overrightarrow P_v$$

---

6 线性插值

线性插值可能是图形学中最为常见的思想和计算操作了，回顾我们之前的带参数的2D直线，$p(t)=p_0+t(p_1-p_0)$，即$p(t)=(1-t)\cdot p_0+t \cdot p_1$,其实可以认为是在点$p_0,p_1$之间线性插值，权重为$t$.

更通用的一种情形，有$n+1$个散点，对应的$x$坐标$x_0,x_1 … x_{n-1},x_n$,对应的y值为$y_0,y_1 … y_{n-1},y_n$,此时想得到一条连续的函数$f(x)$,就可以通过在相邻的散点插值得到：

$$f(x)=y_i+\frac{x-x_i}{x_{i+1}-x_i}(y_{i+1}-y_i) \text {,(此时的$t=\frac{x-x_i}{x_{i+1}-x_i}$)}$$

---

7 三角形

无论是2D三角形还是3D三角形，都是各种图形学程序中的基础模型图元(modeling primitive)。比如三角形的Color图元，只有3个顶点(Vertex)有Color值，三角形内的其他值则通过插值方法得到，通常直接采用重心坐标插值(barycentric coordinates)。

本节将分别讨论2D和3D三角形。

7.1 2D三角形

对于一个2D三角形，三个顶点为$a,b,c$，则可以立马通过向量叉乘($S=\frac {1}{2} \vec{ab} \times \vec{ac}$)得到它的面积： $$S = \frac {1}{2} \left | \begin{array}{ccc} x_b-x_a    & x_c-x_a\\ y_b-y_a  & y_c-y_a \\ \end{array} \right |= \frac {1}{2}(x_a y_b+x_b y_c+x_c y_c-x_a y_c-x_b y_a-x_c y_b)$$ (该公式的推导可以参考本书章节$Chapter5.Linear Algebra-5.3$.注意,考虑到叉乘的方向性，$a,b,c$三个点要成逆时针排列，否则得到面积的相反数.) 三角形的坐标插值，基本原理还是来自于平行四边形规则的向量合成，即使2个向量不平行，同样可以作为向量基。 首先，对于三角形所在平面内的任意点$p$,满足： $$p=a+\beta \vec{ab} + \gamma \vec{ac}=a+\beta (b-a) + \gamma (c-a)=(1-\beta -\gamma)a+\beta b+\gamma c$$ 为方便计算书写，令$\alpha \equiv 1-\beta -\gamma$,则$p(\alpha,\beta,\gamma)=\alpha a + \beta b +\gamma c.$ 注意，点$p$位于三角形内部的充要条件为: $\alpha, \beta,\gamma \in (0,1)$. 回顾2.5.2节隐式2D直线的内容，平行于直线$f(x,y)=0$的其他直线的函数值$f(x,y)$大于或小于0，分布于$f(x,y)=0$的两侧。如下图所示，我们规定$f_{ac}(x,y)=0$,且点b所在平行线$f_{ac}(x,y)_{\beta}=1$.

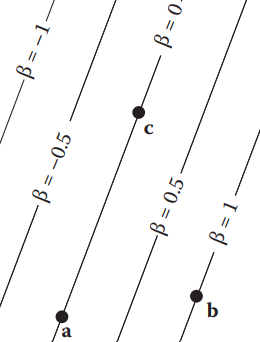
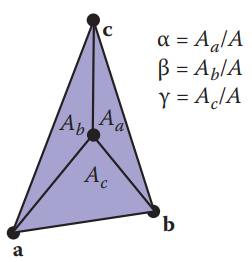
那么在线段$ab$上的点$(x,y)$，$\beta$值为： $$\beta=\frac{f_{ac}(x,y)}{f_{ac}(x_b,y_b)}$$ 基于隐式2D直线章节的内容，ab直线可表示为： $f_{ab}(x,y)\equiv (y_a -y_b)x +(x_b-x_a)y + x_a y_b -x_b y_a=0$. 则相对应的$\gamma$值为： $$\gamma =\frac {(y_a -y_b)x +(x_b-x_a)y + x_a y_b -x_b y_a}{(y_a -y_b)x_c +(x_b-x_a)y_c + x_a y_b -x_b y_a}$$ 同理，可计算得到点b对应的$\beta$值,最后$\alpha=1-\beta -\gamma$. 值得注意的是，$\alpha,\beta,\gamma$值表征的是$f(x,y)的值，隐式地表征$点p到各条边的距离，所以，点p和三个顶点行成的3个小三角形和大三角形的比值其实就是$\alpha,\beta,\gamma$,即如下图所示：

7.2 3D三角形

对于上一节得到的2D三角形插值公式完全适用于3D三角形$abc$,同样有： $$p=(1-\beta -\gamma)a+\beta b+\gamma c$$ 三角形$abc$，三条边对应3个比例$\alpha,\beta,\gamma$,则对于三角形内任意点$p$: $$\alpha =\frac{Area_{pbc}}{Area_{abc}}=\frac{\lVert (c-b)\times(p-b) \rVert} {\lVert (b-a)\times(c-a) \rVert}$$ 令$\vec n=(b-a)\times(c-a)$,$\vec n_a =(c-b)\times(p-b)$，因为两者平行且同向($\vec n \cdot \vec n_a=||\vec n|| \cdot ||\vec n_a||$),则上式可化简：

$$\alpha =\frac{\lVert \vec n_a \rVert}{\lVert \vec n \rVert }= \frac{\lVert \vec n_a \rVert \cdot \lVert \vec n \rVert }{\lVert \vec n \rVert \cdot \lVert \vec n \rVert } =\frac{\vec n \cdot \vec n_a }{ { \lVert \vec n \rVert }^2 }$$

同理可得$\beta, \gamma$的值：

$$\beta =\frac{\vec n \cdot \vec n_b}{ {\lVert \vec n \rVert }^2}$$ $$\gamma =\frac{\vec n \cdot \vec n_c}{ {\lVert \vec n \rVert }^2}$$

其中，$n_b =(a-c)\times(p-c)$，$n_c =(b-a)\times(p-a)$. $$\text{——————– Chapter2(完结) @2021-12-19 ——————–}$$